Mathematics Notes - Theory of Knowledge

Mathematics Quotes
- "Mathematics is the abstract key which turns the lock of the universe" (John Polkinghorne).
- "Everything that can be counted does not count. Everything that counts cannot be counted" (Albert Einstein).
- "A mathematician is a machine for turning coffee into theorems" (Paul Erdos).
- "When you have satisfied yourself that the theorem is true, you start proving it" (Arthur Koestler).
- "If mathematics describes an objective world just like physics, there is no reason why inductive methods should not be applied in mathematics just the same as in physics" Kurt Godel).
- "On each decision, the mathematical analysis only got me to the point where my intuition had to take over." (Robert Jensen)
- "Mathematics is the most beautiful and most powerful creation of the human spirit." (Stefan Banach)
- "The essence of mathematics lies in its freedom" (Georg Cantor).
- "The mathematics is not there till we put it there" (Arthur Eddington).
- "Logic and mathematics are nothing but specialized linguistic structures" (Jean Piaget).
- "Film is one of the three universal languages, the other two: mathematics and music" (Frank Capra).
Mathematics Definitions
- "The abstract science of number, quantity, and space, either as abstract concepts (pure mathematics), or as applied to other disciplines such as physics and engineering (applied mathematics)." (Oxford Dictionary)
- "The science of numbers, quantities, and shapes and the relations between them." (Merriam Webster Dictionary)
- "The systematic treatment of magnitude, relationships between figures and forms, and relations between quantities expressed symbolically." (Dictionary.com)
- "The study of the measurement, properties, and relationships of quantities and sets, using numbers and symbols." (The Free Dictionary)
Is math created or discovered?
Eugene Wigner said “The miracle of the appropriateness of the language of mathematics to the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve.” This quote pulls out several aspects of this created versus invented discussion. All phenomena observed in classical electricity and magnetism can be explained by means of just four mathematical equations (Livio). In some cases, Math seems to be so perfectly in-line with natural reality that it must be discovered. Whereas there are other examples of Math where there is no clear relation to reality, suggesting that math is invented. But Mario Livio explains that, "mathematicians [have] developed abstract branches of mathematics with absolutely no applications in mind; yet decades, or sometimes centuries later, physicists discovered that those theories provided necessary mathematical underpinnings for physical phenomena." This again suggests that mathematicians are discovering math.
Also, some theories (explanations of reality) can be mathematically correct, but not correct in the real world. Zeno's Paradox is an example of this. Here's the story:
Zeno’s Paradox: Achilles and the tortoise
- The question was posed: How could a tortoise beat greek legend Achilles in a race? Philosopher Zeno attempted to answer such a question.First, the tortoise is given a head start.
- So, when the race starts, Achilles will have to make up the distance.
- However, in that time, the tortoise would have moved forward by a little bit.
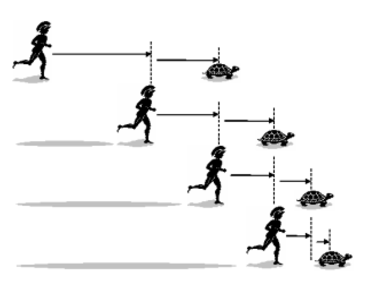
- Then Achilles will have to make up that distance, but in that time the tortoise would have had to move even more.
- Therefore Achilles would never be able to pass the tortoise and the tortoise would win the race.
- Will this theory may seem mathematically correct, we know that in reality, it is impossible. This is an example of how while something things can be explained mathematically, they cannot always be true.